Unas jugadoras de basket no tan parecidas (enseñanza de la dispersión)

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Partido de basket. Queda un minuto y el entrenador tiene que decidir a qué jugadora sacar. ¿A quién elegirá?

• Si va perdiendo de 8 puntos.
• Si va ganando de 2 puntos.

Dentro hilo con secuencia de aula sobre dispersión con pinceladas de didáctica de las matemáticas.

Con este hilo participo en el #HilosDC6.

Esto de la dispersión nos servirá como excusa para diferenciar una enseñanza para la resolución de problemas de una enseñanza a través de la resolución de problemas. Y esto sirve tanto para primaria como para secundaria.

Esto de la dispersión nos servirá como excusa para diferenciar una enseñanza para la resolución de problemas de una enseñanza a través de la resolución de problemas. Y esto sirve tanto para primaria como para secundaria.

Por ubicarnos, las medidas de dispersión aparecen como contenido curricular por primera vez en 2º ESO (13-14 años). Luego hablaremos sobre currículo, libros de texto y otras cosas del montón. Ahora, me centraré en presentar la secuencia de aula

A ver si vais a pensar que soy super original. No. Esta actividad que voy a contar está sacada prácticamente tal cual de la Guía Praxis, que fue coordinada por Carmen Azcárate y Jordi Deulofeu. Lo que he hecho simplemente es darle una razón de ser con las preguntas iniciales.

¿Se podría decir que es innovación? Yo creo que sí, aunque tiene tela decir que sigue siendo innovación algo sacado de una guía de finales de los 90. Pero es que queda mucho por hacer. Y vamos a usarla también para hablar de resultados de investigación.

Esto lo he hecho este curso en una clase de 2º ESO donde ya empiezan a estar habituados a trabajar A TRAVÉS de la resolución de problemas. Lo ideal aquí es tener al alumnado en parejas o grupos de hasta cuatro.

Luego profundizaré en eso de A TRAVÉS y las alternativas que hay. De momento, basta decir que se trata de presentar tareas (situaciones-problema) al alumnado, de manera que los contenidos emerjan conforme se avanza.

Podría decirse que es una enseñanza de descubrimiento guiado. Ello no implica dejar a los alumnos solos, sino que se para la clase cada cierto tiempo para hacer puestas en común y que el profesor negocie los significados de los objetos matemáticos que van apareciendo.

La tarea que va a motivar todo es la del primer tweet. Es una decisión que debe tomarse considerando los datos disponibles. ¿Sacamos al mismo tipo de jugadora cuando vamos ganando por poco que cuando el partido está prácticamente perdido, pero con alguna posibilidad de ganar?

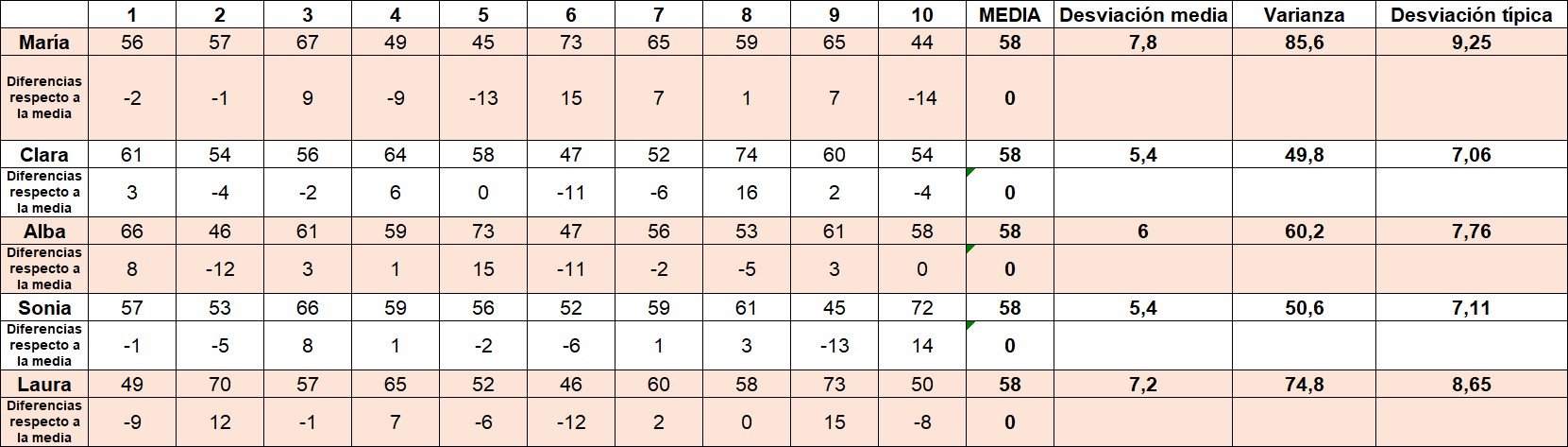
¿Y qué datos son esos? Nada más que el porcentaje de aciertos de tiro exterior de cinco jugadoras durante los últimos diez partidos. Es decir, esta tabla. ¡Cuánto número! Algo habrá que hacer…

Aquí se puede mencionar cómo ha cambiado el baloncesto en los últimos años, y por qué equipos como los Golden State Warriors tiran tantos triples (y les ha ido bastante bien).

Primera pregunta, para entrar en calor y ver que hemos entendido el contexto. Y que va a tener miga. ¿En qué partidos consigue Alba un % por encima de sus compañeras? ¿Solo en los que sea la mejor de todas? ¿O en los que esté por encima de la media?

Ya que hablamos de la media, ahora vamos a calcular la media de los porcentajes de acierto para cada jugadora. ¿Qué observamos? Pues que todas las jugadoras… ¡tienen la misma media!

¿Qué hacer? El entrenador está en un aprieto… Ya que tenemos datos, vamos a tratar de representarlos gráficamente, a ver si con eso podemos decir algo. Se les proporciona a los alumnos el diagrama de puntos de una jugadora y se les deja trabajar y discutir a qué jugadora sacar.

Resulta que visualmente no se aprecia cuál es más regular, más fiable. En la puesta en común unos grupos defienden a Clara, otros a Sonia… Seguimos necesitando algo más.

En estas puestas en común a veces pasan cosas maravillosas. En un grupo decidieron emplear un código de colores y mostrar a todas las jugadoras en el mismo diagrama de puntos. Discutimos sobre si es más adecuado o no. Parece que se ve más claro por separado.

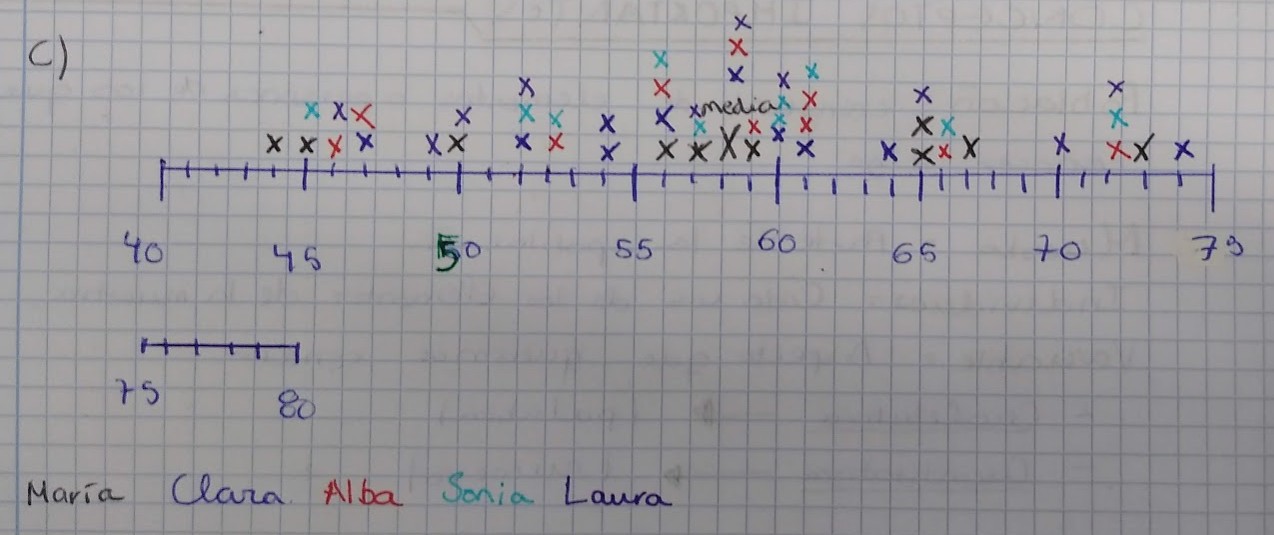
Sin embargo, tiene la ventaja de que te asegura la misma escala para todas las jugadoras. También, que los diagramas estén alineados para facilitar la inspección visual. En la foto vemos este error de representación.

Vamos ahora a medir, esto es, a asignar un número a cada jugadora, a cada uno de los diagramas de puntos. Lo más fácil es calcular la anchura. Esto se llama rango. ¡Todas lo tienen muy parecido! María, quizás, un poco más alto…

Pero… ¿qué pasaría con una jugadora que durante 8 días encestase el 58% de los tiros, pero un día le saliese malo y tuviese un 31% y otro día hiciese un gran partido con un 75% de acierto? ¿Cuál es su rango? ¿Su diagrama de puntos? ¿Es más o menos fiable que las anteriores?

Si lo comparamos con el de Sonia, por ejemplo, vemos que el de la nueva jugadora está mucho más concentrado en torno a la media, salvo esas dos excepciones. El de Sonia está más extendido. Atención a los gestos que hacen las jugadoras en los gifs.

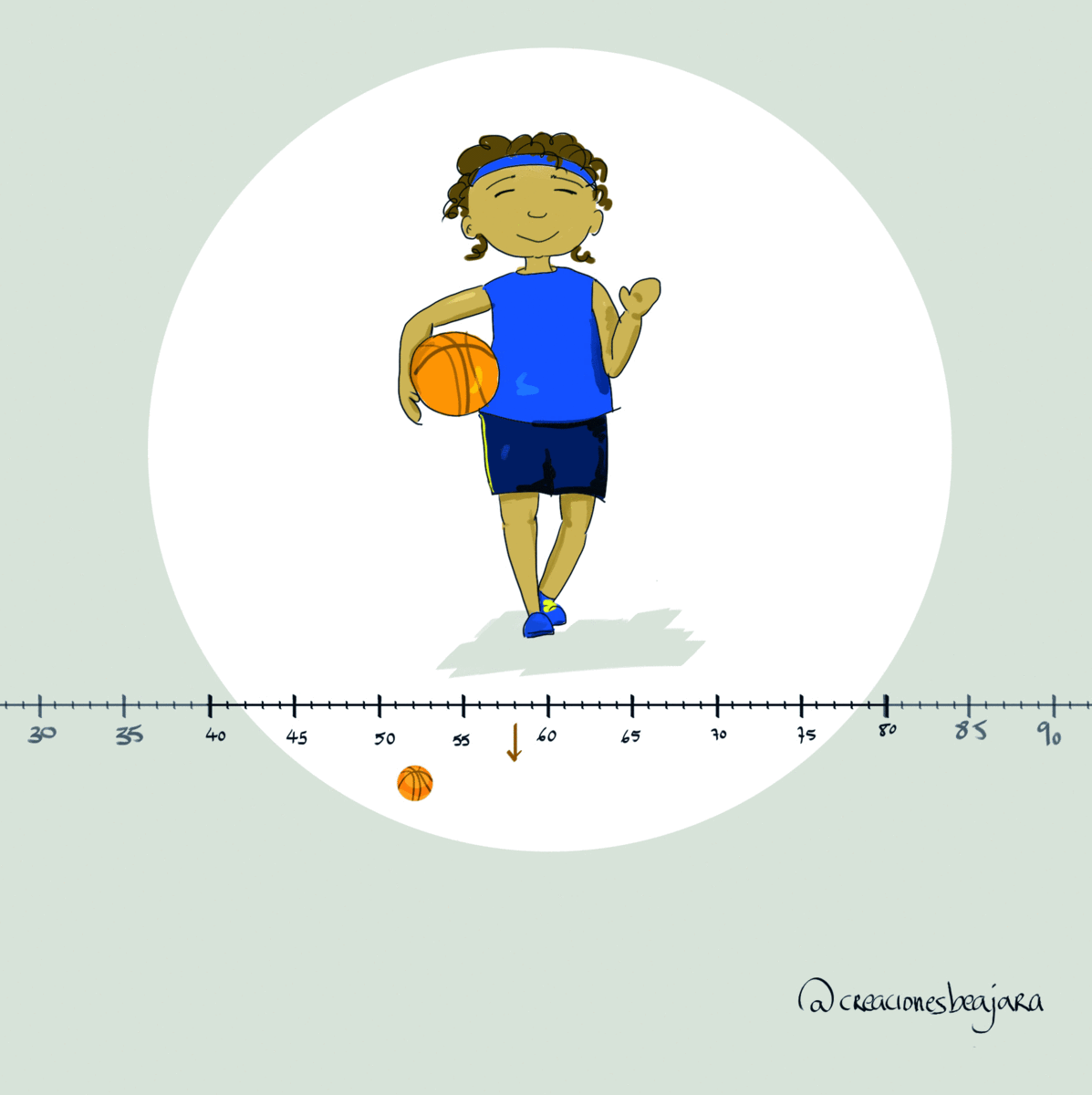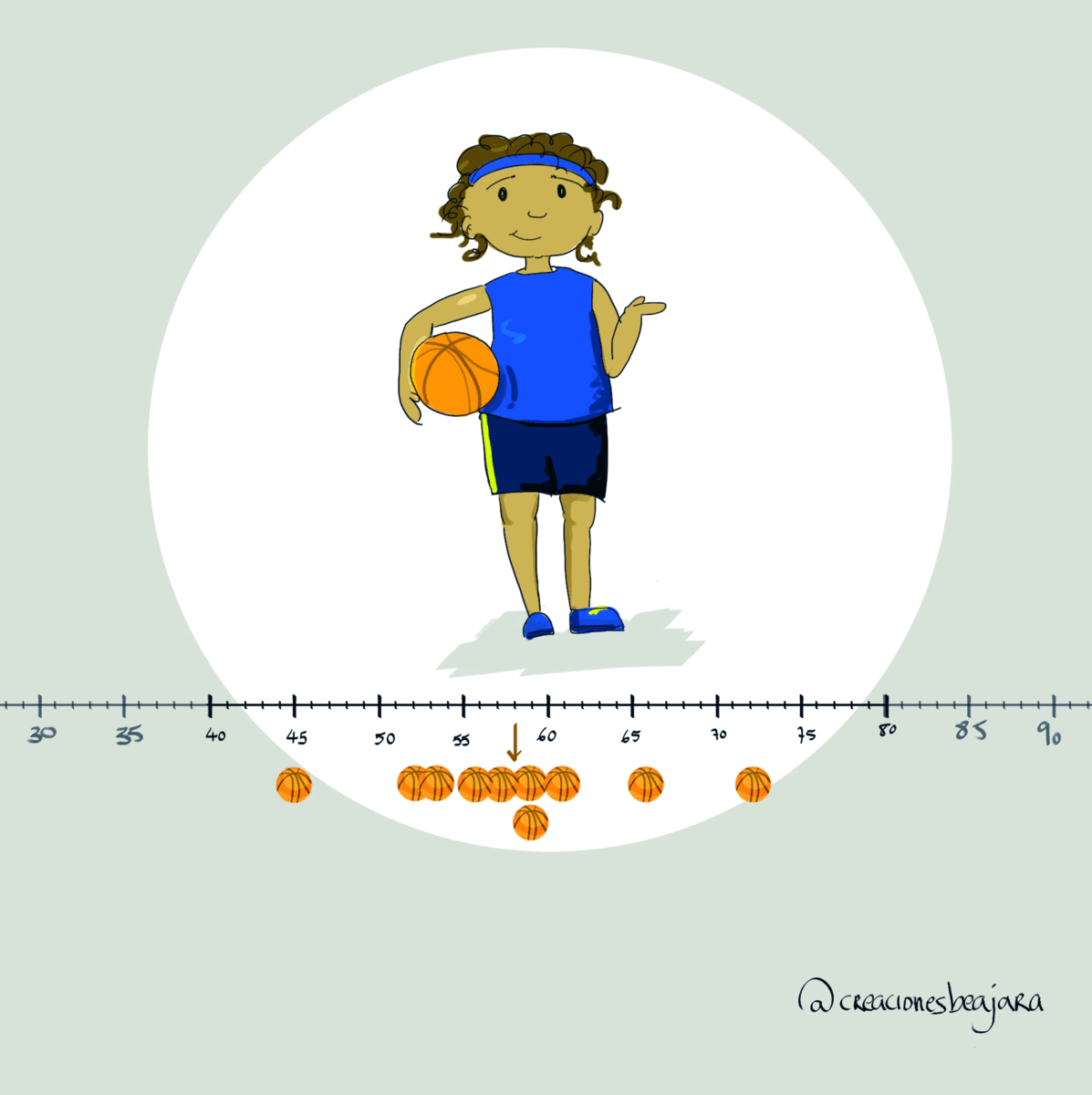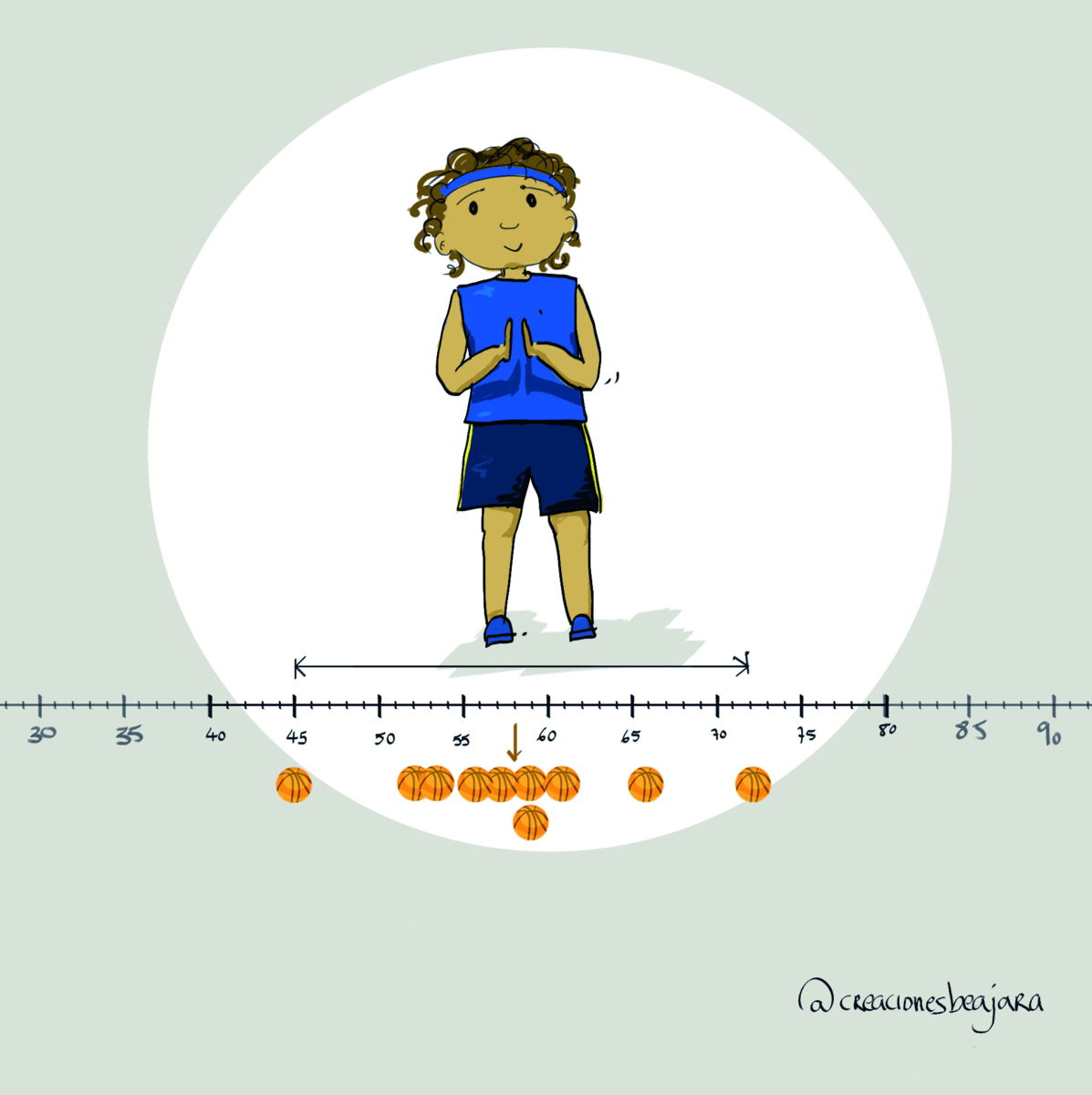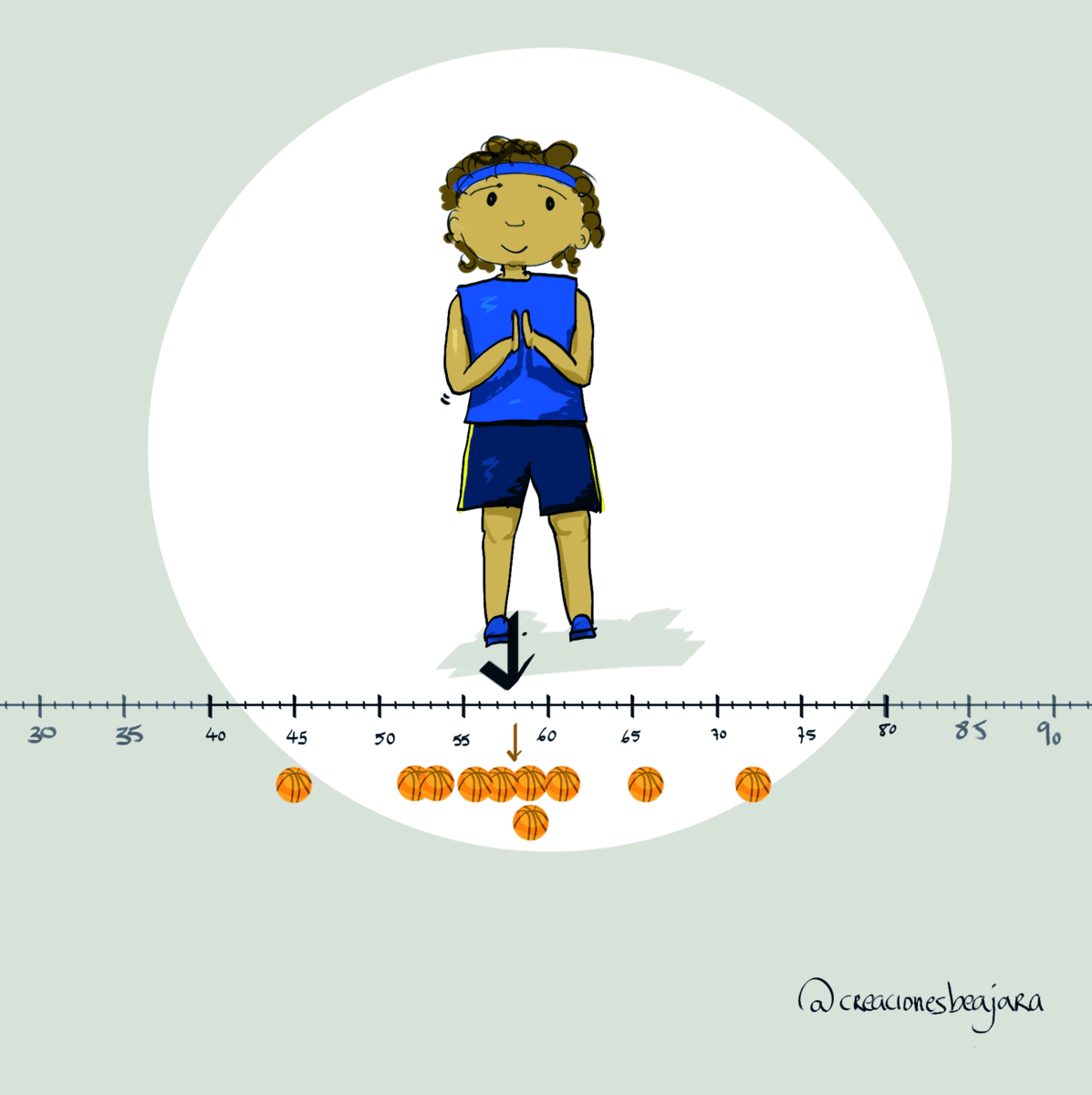
Está claro entonces que el rango se queda corto y que necesitamos una medida mejor de la dispersión. No puede ser que una jugadora que tenga un rango de casi el doble sea más regular, fiable, menos dispersa. El rango, como medida, es una castaña.

El lenguaje, en sentido amplio, no solo verbal, es un elemento muy importante en todos los marcos teóricos en didáctica de la matemática. La articulación de diferentes registros y representaciones lingüísticos (verbal, gráfico, simbólico…) en indicador de una alta idoneidad.

Los gestos no son una excepción y son parte de la actividad. Abriendo o cerrando los brazos, como en los dibujines, damos una idea de rango y dispersión. De hecho, los gestos ocupan un lugar de privilegio en enfoques teóricos como el Semiotic Bundle.

A lo que íbamos, necesitamos algo mejor que el rango. Así que planteamos medir las desviaciones de cada jugadora respecto a la media. Sin embargo, al sumarlas ocurre algo ¿inesperado?

Digo que puede ser inesperado si no se trabajan las propiedades de la media en 1º ESO o antes de esta secuencia. En 1º hemos visto cómo hacer un diagrama de barras buscando cierta media. Es el principio de las gallinas que entran por las que salen.

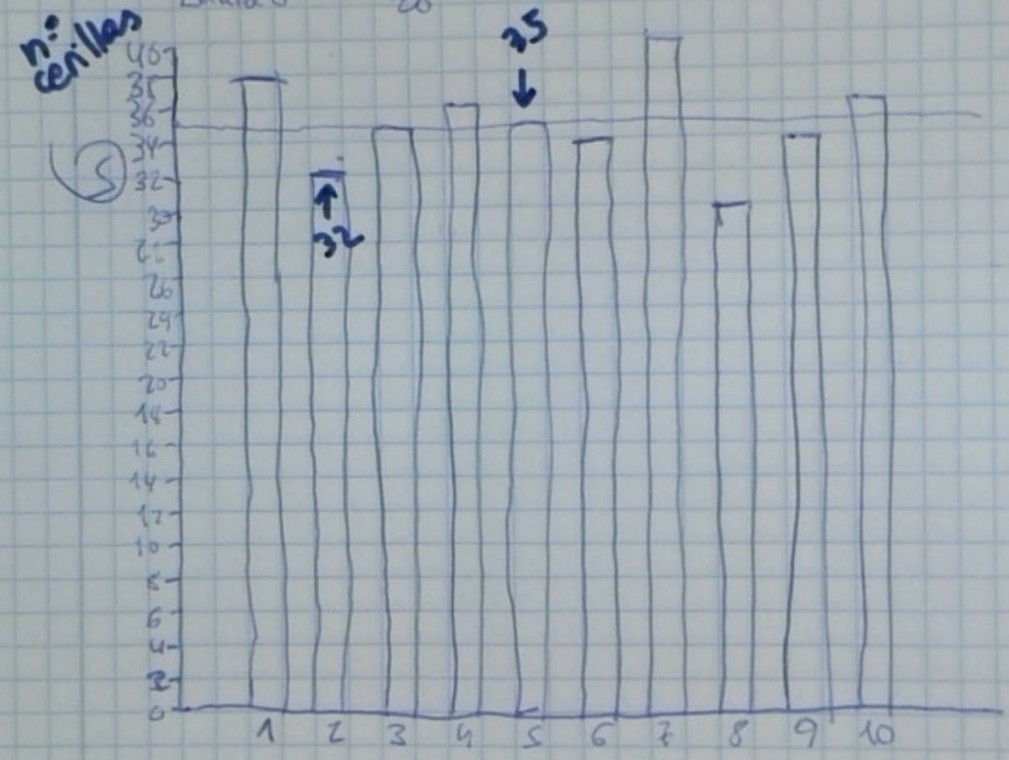
«Un anuncio de cajas de cerillas indica que el número medio de cerillas por caja es 35. Representa una gráfica de una posible distribución del número de cerillas en 10 cajas, de modo que la media sea igual a 35»

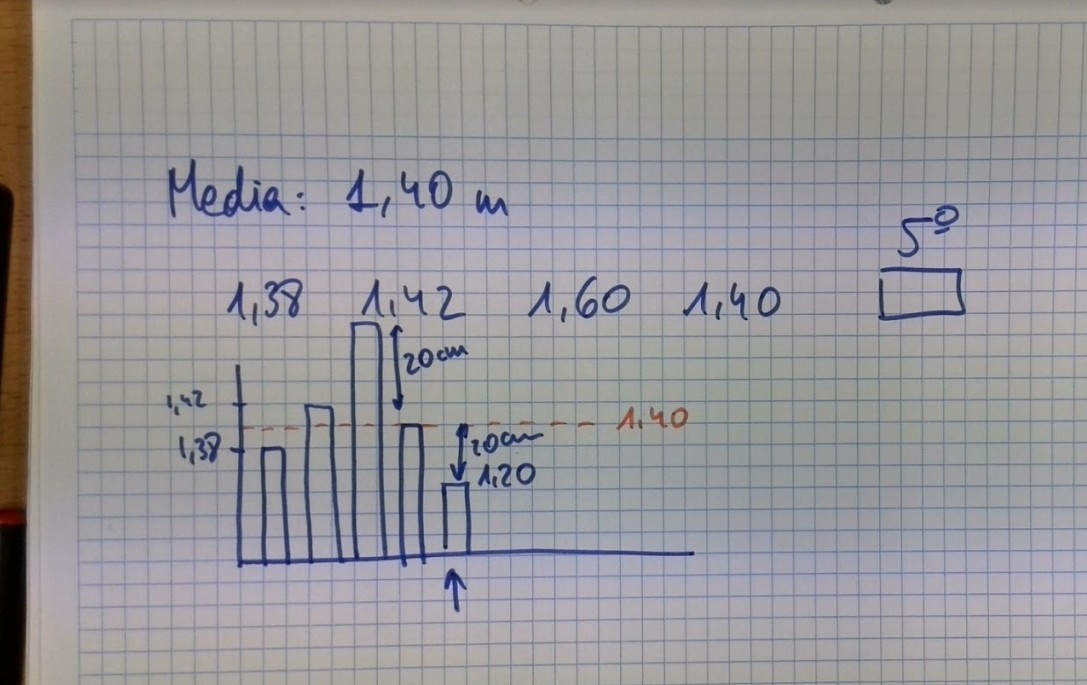
«La altura media de los alumnos de un colegio es 1,40. Si extraemos una muestra aleatoria de 5 estudiantes y resulta que la altura de los 4 primeros es de 1,38, 1,42, 1,60, 1,40. ¿Cuál sería la altura más probable del quinto estudiante?»

Estas dos últimas actividades se han seleccionado de los apuntes de Análisis de datos y su didáctica, de Batanero y Godino. En esta referencia se muestran tipos de actividades para englobar las diferentes propiedades de la media.

Por cierto, estas capturas las estoy tomando con un visor de documentos. Desde que vi los tweets de @followero al respecto no hago más que verle potencial. Así puedo mostrar la producción de un alumno a todos y corregirla en vivo, o explicar sobre mi cuaderno, entre otras cosas.

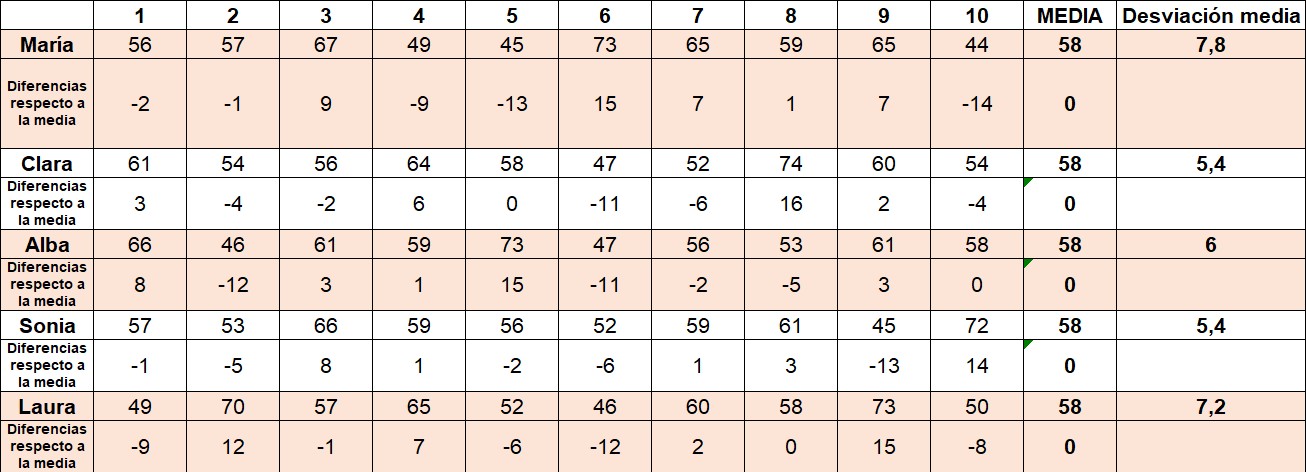
Volviendo al lío. La suma de las diferencias respecto de la media sale cero para cualquiera de las jugadoras. Es una propiedad de la media. Tiene sentido, pues, considerar la distancia a la media. Y hacer un promedio de estas. Así obtenemos la desviación media para cada jugadora.

Si ordenamos a las jugadoras de esta manera vemos que la menos regular es María (DM=7,8), y que las más regulares (menos dispersas) son Sonia y Clara (DM=5,4). En la puesta en común hablamos de qué significan ese 7,8 y esos 5,4.

Ahora consideramos el caso de una jugadora, Berta, que ha estado lesionada durante 2 partidos. Durante los otros 8 partidos ha acumulado una cantidad de dispersión de 67. ¿Es más regular que María?

Ninguna tarea está puesta al azar. Si dividimos 67 entre 10, obtendríamos una DM de 6,7, concluyendo que es más fiable Berta. Ahora, ¿hemos tenido en cuenta que no ha jugado dos partidos?

• Ah, es que habrá que dividir para 8, ¿no?
• Entonces sale… 8,375, no es nada regular.

Y llegamos a la varianza. A los alumnos les hace gracia esta palabra.

• Sí, varianza. Con zzzzeta.

Toca proponer considerar los cuadrados de las desviaciones, como otra estrategia. Es un punto que, de entrada, puede parecer tener poco sentido, si ya tenemos la desviación media.

Sí, aparece un poco forzado, pero tiene alguna ventaja. Como que los datos que se alejen más de la media van a tener un peso algo mayor en la medida de la dispersión. En nuestro ejemplo, nos ayudan a desempatar entre Sonia y Clara como jugadoras más fiables.

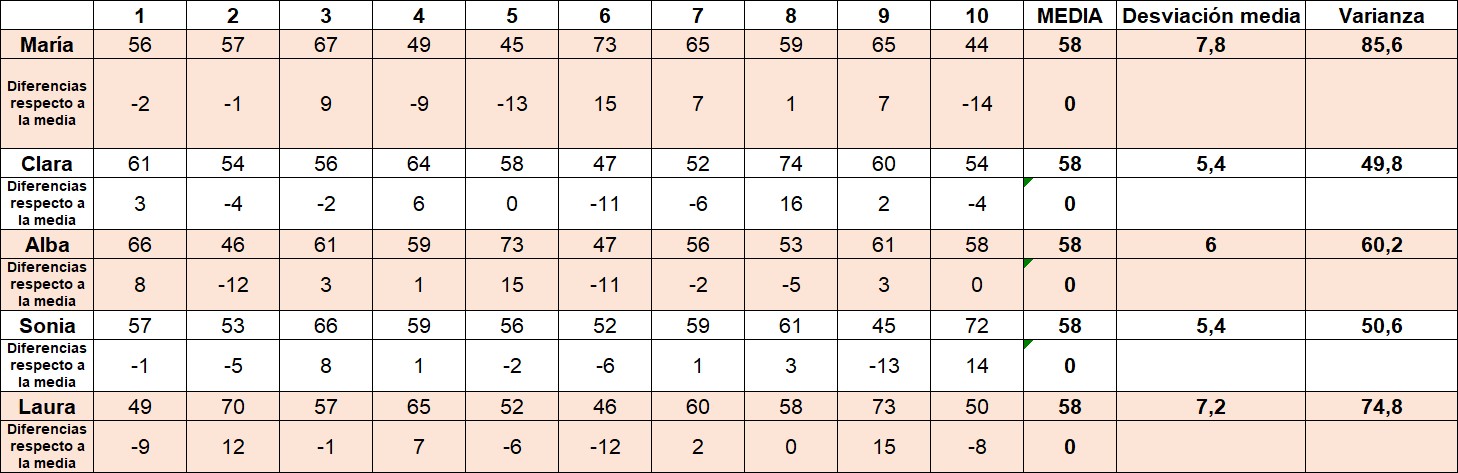
La más regular, la menos dispersa, es Clara. A la hora de interpretar esa varianza de 49 y pico, ¿qué? Al ser desviaciones al cuadrado no podemos decir que lo normal es que se desvíe 49 de la media de acierto. Por eso hacemos la raíz cuadrada para obtener la desviación típica.

Algunos alumnos se apuntan que anulamos el “efecto de elevar al cuadrado”. Señales de que vamos bien son:

• Oye… ¿qué es la dispersión? ¿La varianza?
• ¿No lo sabes? Si llevamos tres días con esto la dispersión.
• Ya…, pero no sé si es la varianza o la desviación típica.

Toca otra puesta en común. Se suelen reservar momentos para ello, pero si surge algo interesante, es el docente el que decide parar la actividad. Podemos decir que la dispersión es lo concentrados o alejados que están los datos respecto de la media (recordamos los gestos).

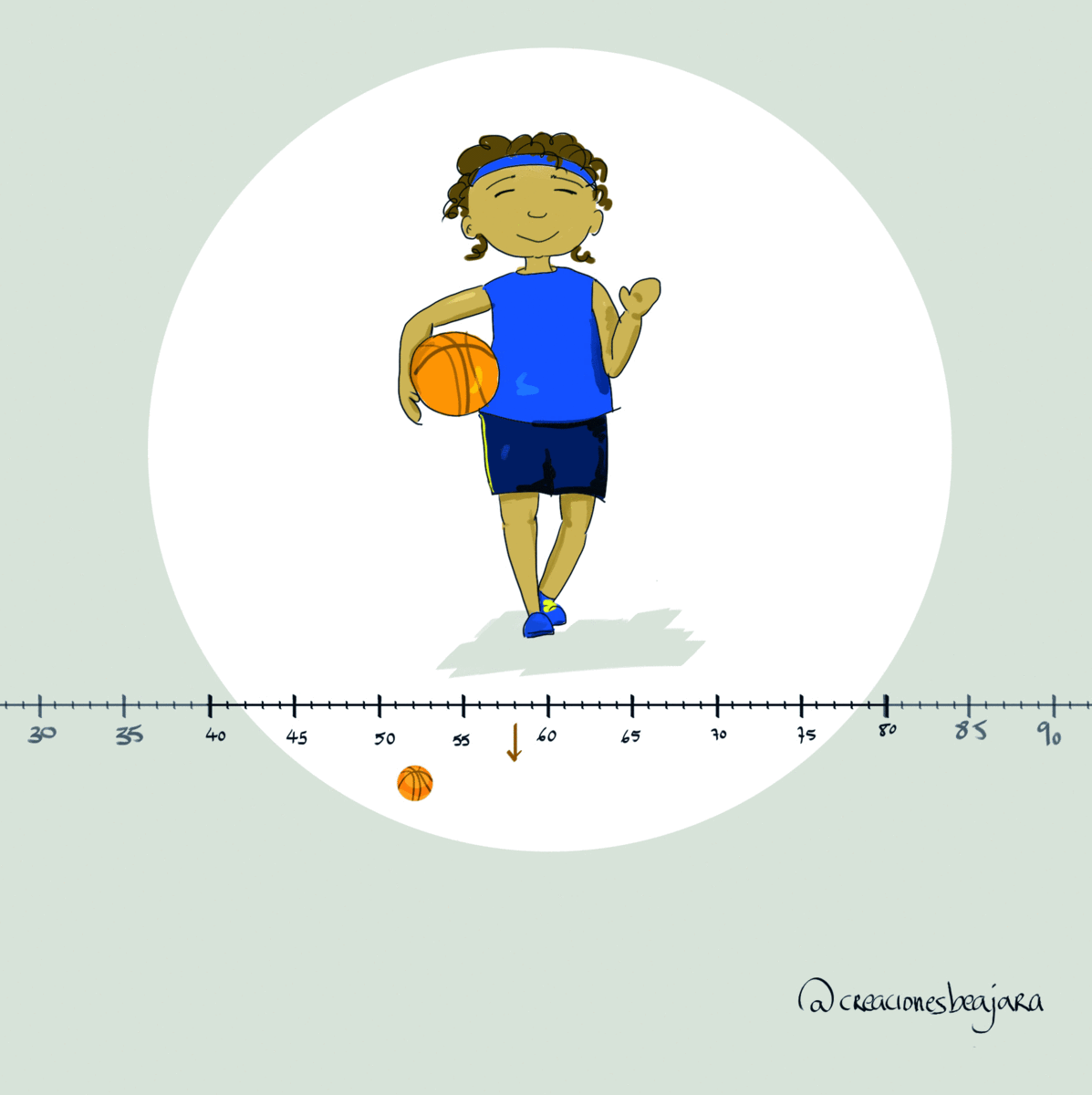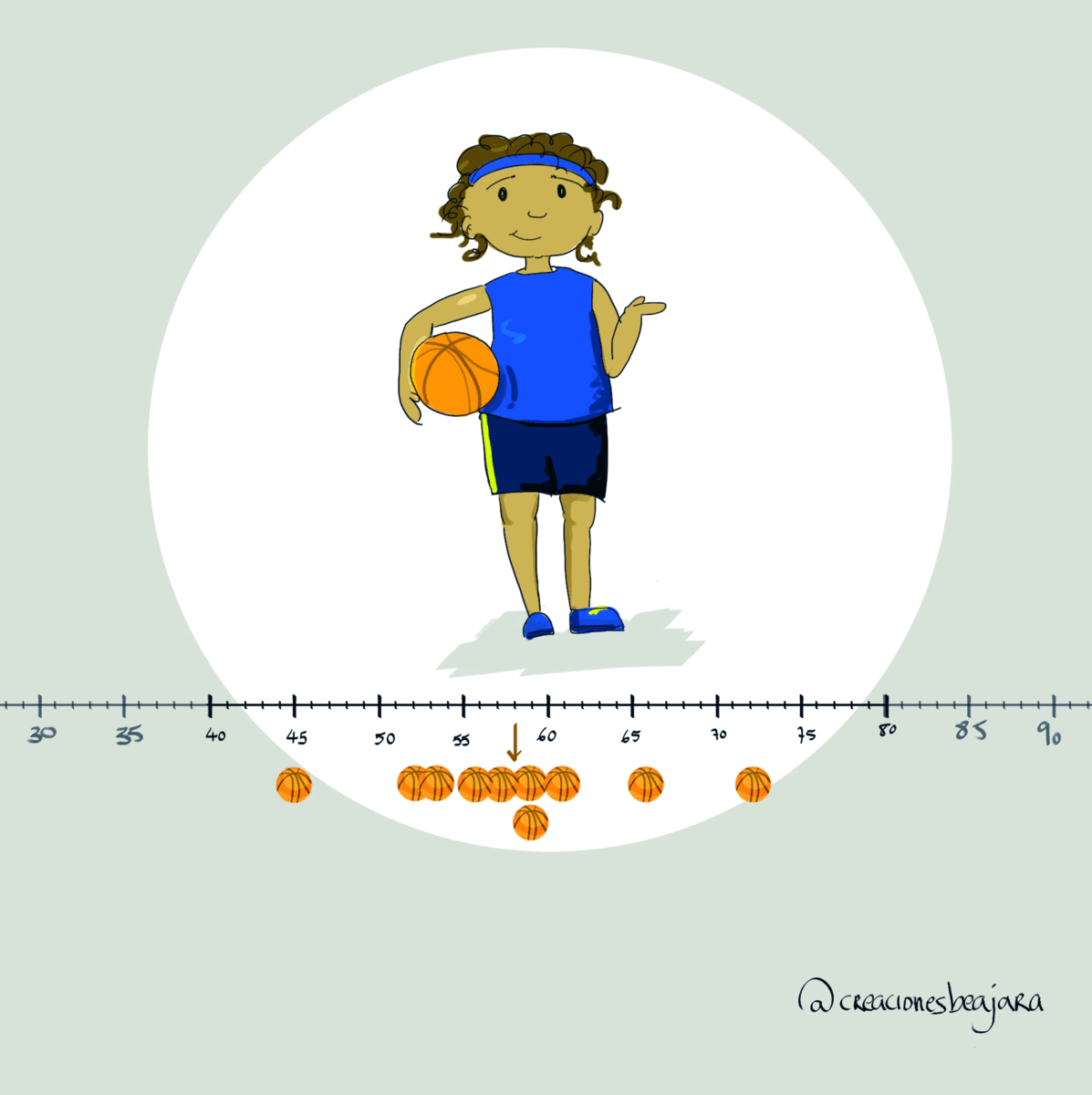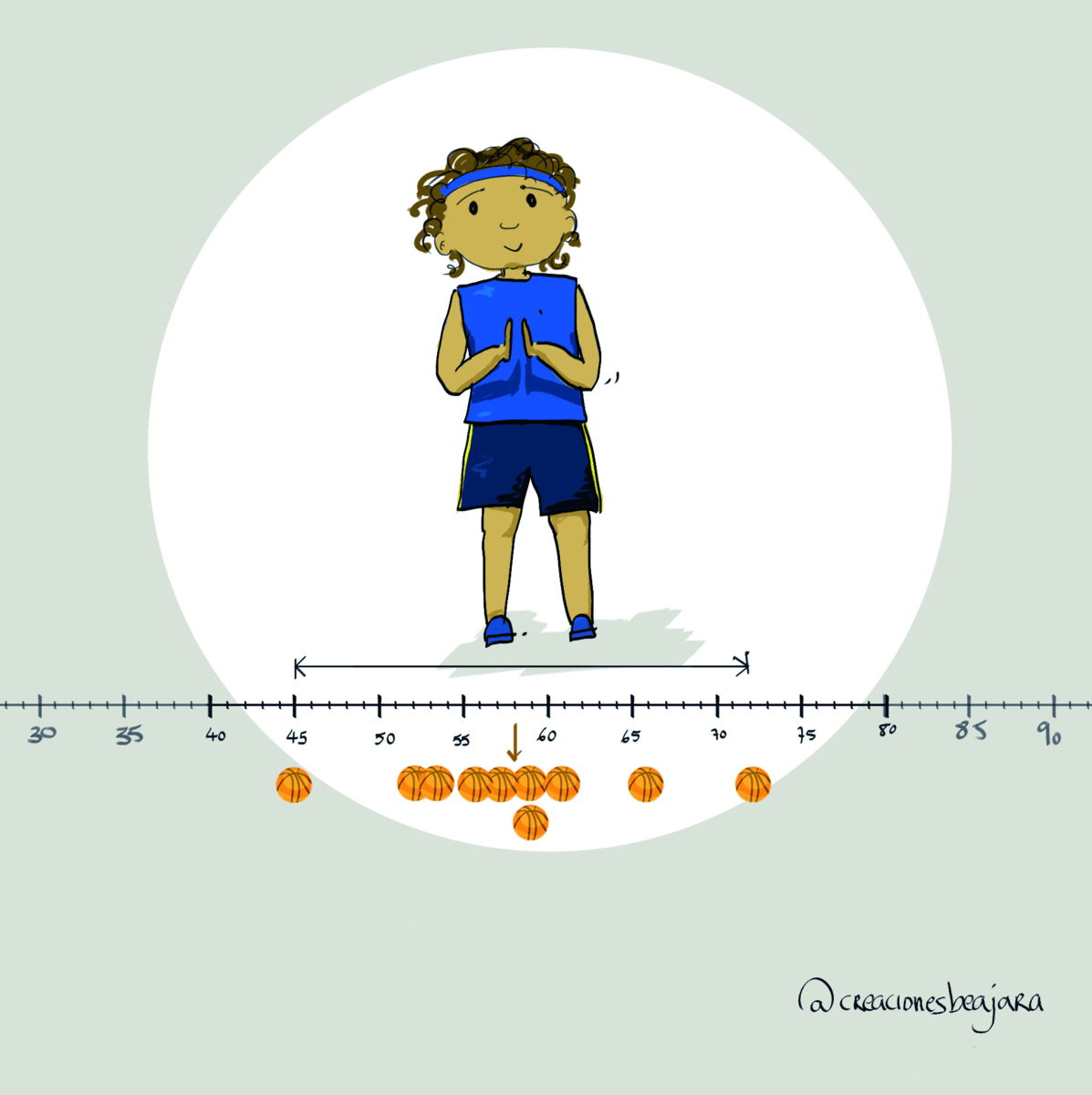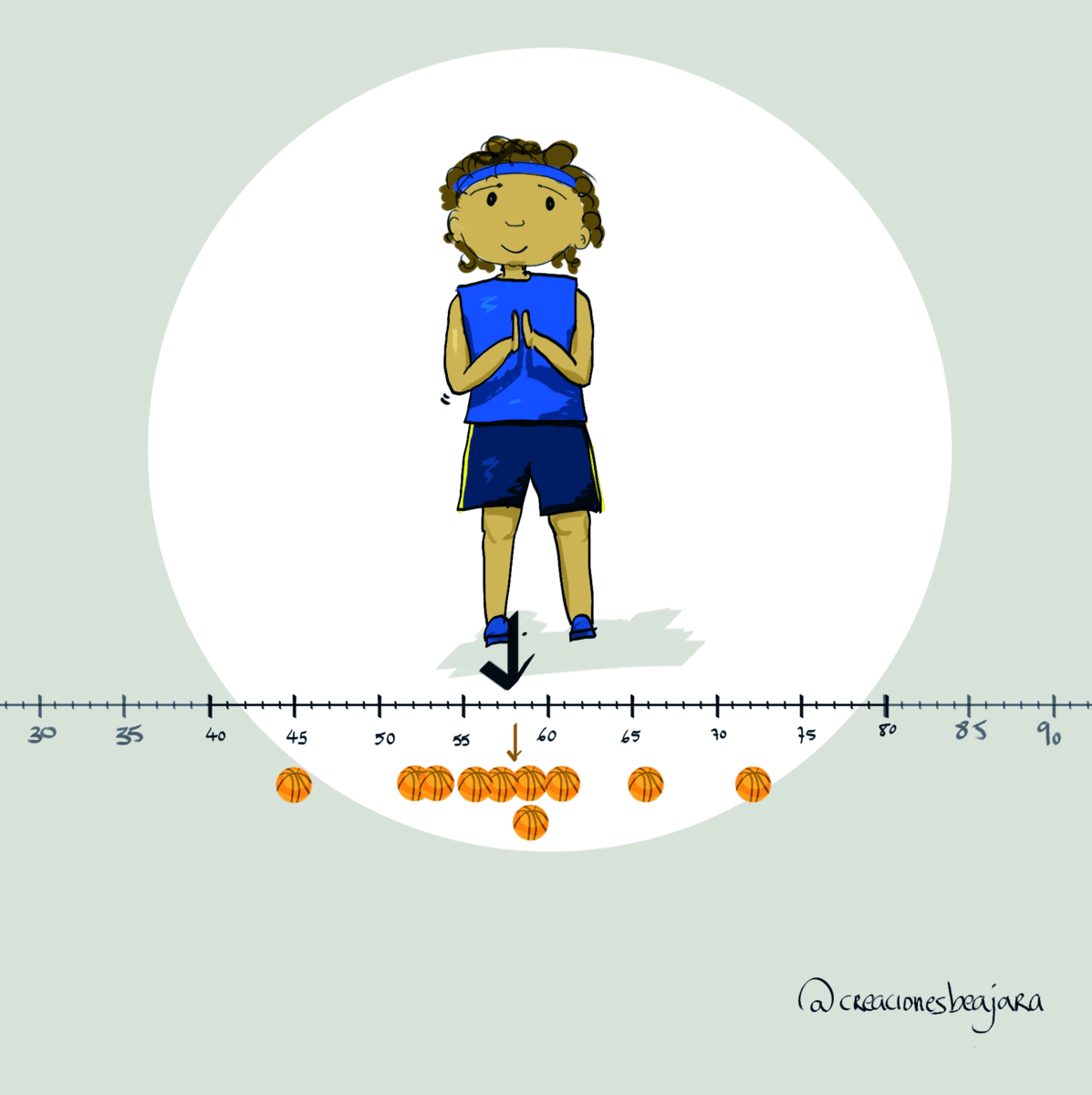
Una cosa distinta es cómo midamos esas dispersión. De hecho, al principio lo hemos hecho sin medir, de forma visual con los diagramas de puntos. Luego, hemos medido el rango, que no vale para mucho. Después, la desviación media, la varianza y la desviación típica.

Entonces… ¿a quién elegimos si queda un minuto y ganamos de 2 puntos? A la más fiable, claro, no queremos pifiarla. El entrenador tiene que sacar a Sonia.

Pero… ¿si vamos perdiendo de 8 puntos? Necesitamos un milagro, no vale con no pifiarla. Sacaremos a María, que teniendo la misma media que Sonia, es mucho más irregular. ¡Le puede salir uno de esos partidos en que mete todo!

O también puede que no. Sin embargo, habremos tomado la decisión adecuada.

Aclaración: los enunciados de todas estas tareas se les dan fotocopiados a los alumnos, que los pegan en el cuaderno.

Estuvimos prácticamente tres días con este problema. Finalmente, la secuencia culmina con un par de actividades de práctica. En el examen, los alumnos se enfrentaron a un problema similar. En una competición de natación, tenemos que elegir al cuarto relevista.

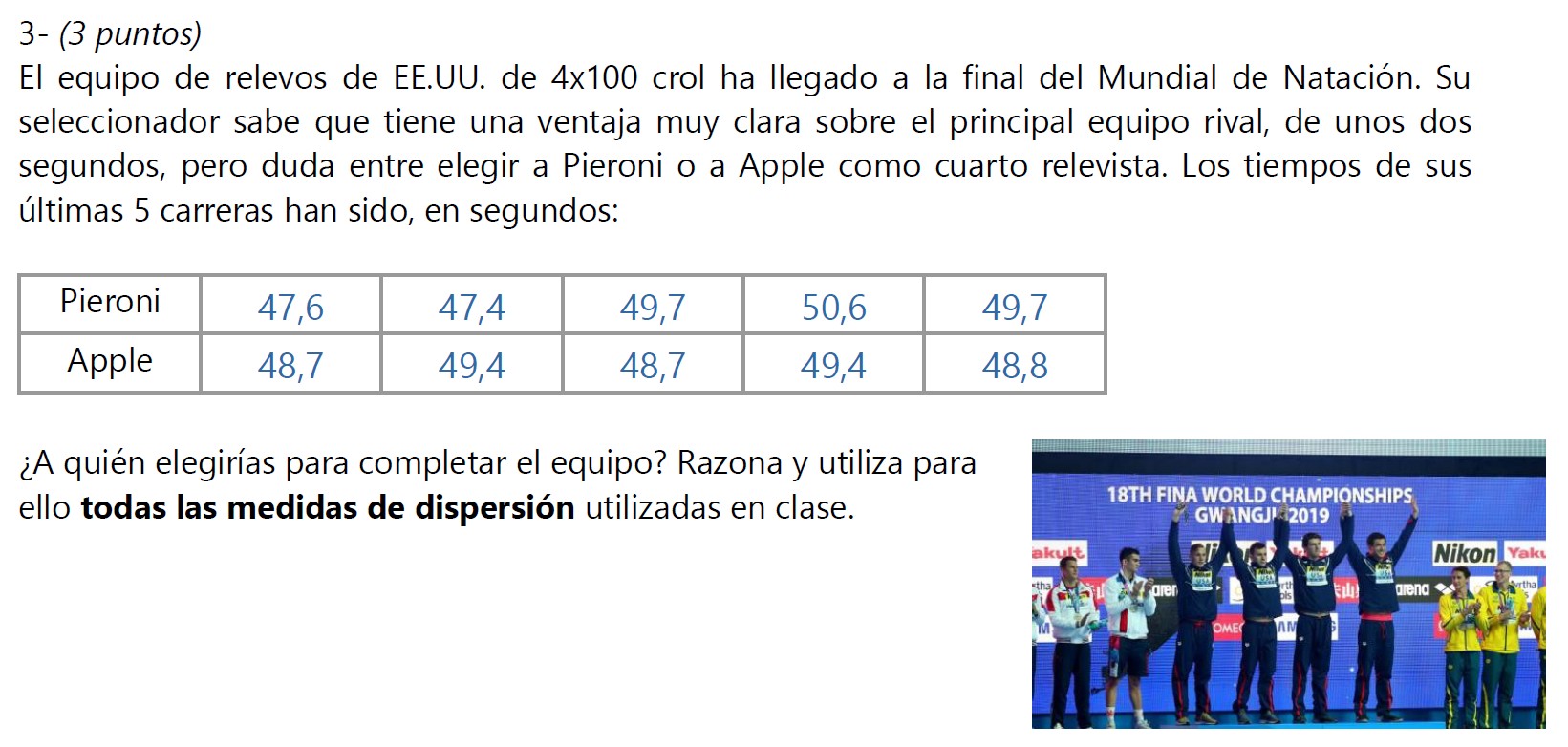
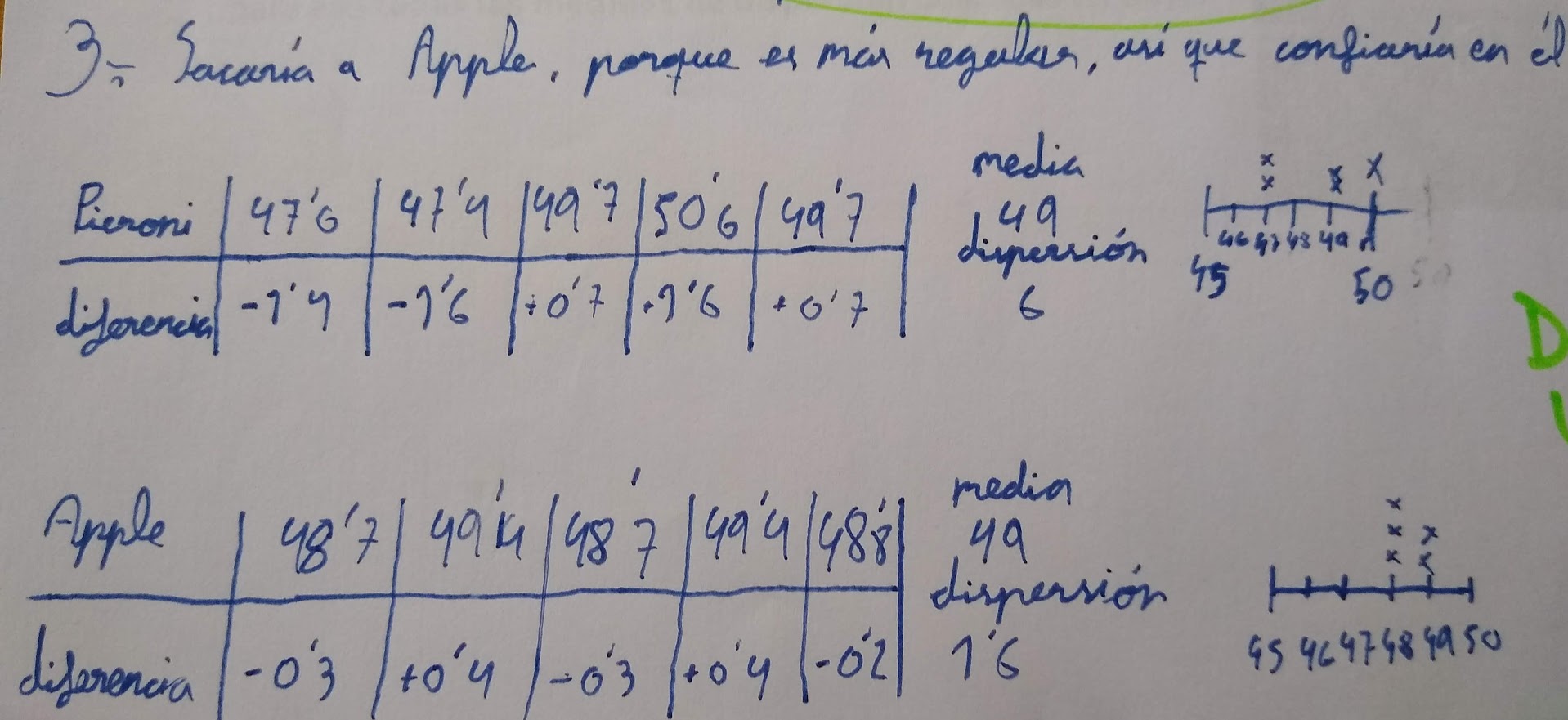
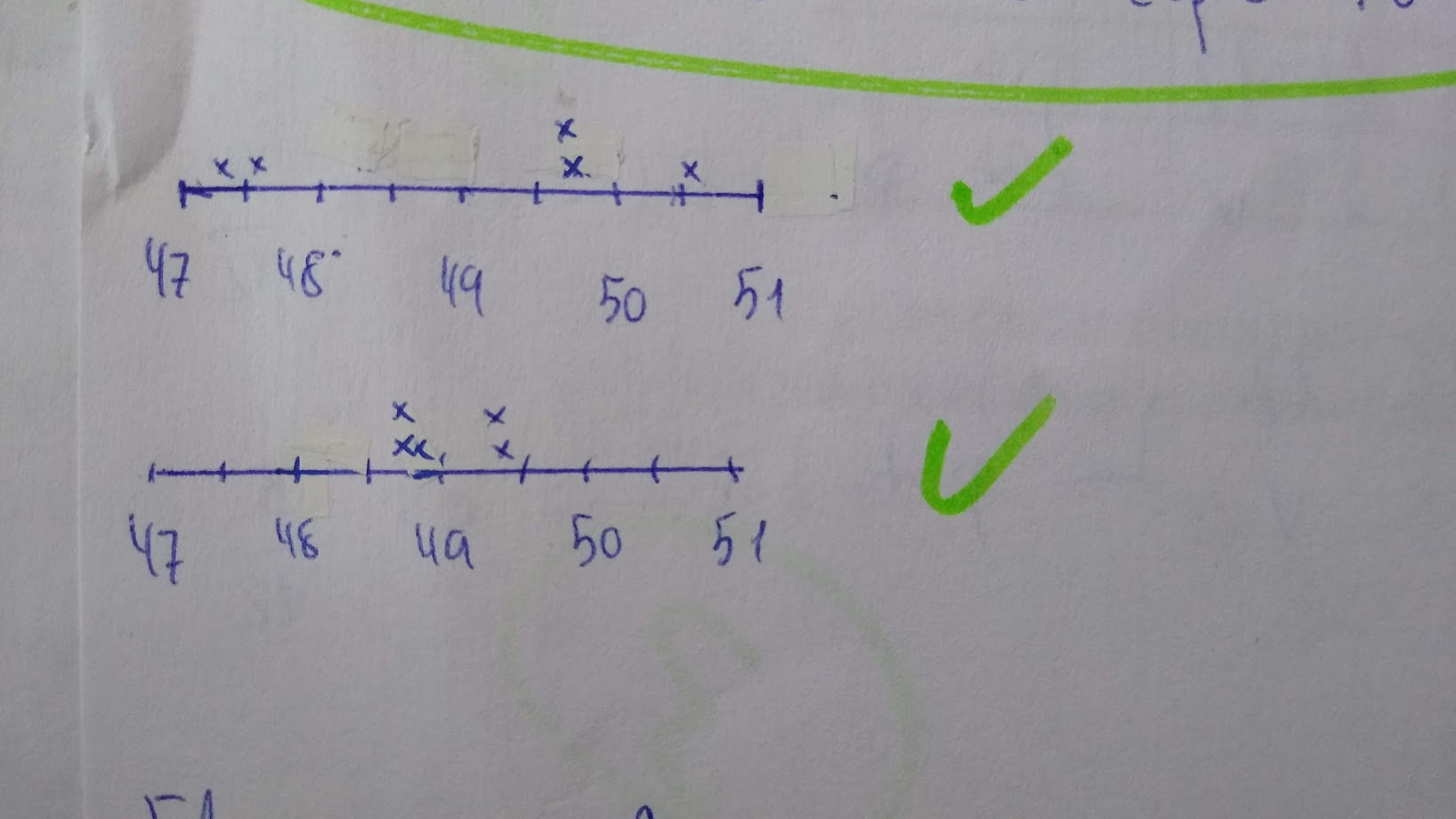
Decía que lo todo esto es enseñanza A TRAVÉS de la resolución de problemas (RP). Si remarco el A TRAVÉS, será que hay otra cosa, ¿no? Porque todos estamos de acuerdo en que la RP es lo más importante, pero hay varias tendencias. Gaulin lo describe bien.

Podemos enseñar SOBRE RP; es decir, técnicas y estrategias, con problemas que tampoco tienen por qué estar muy ligados a ningún contenido. Sin embargo, la alternativa opuesta a la actividad comentada se ubicaría en la enseñanza PARA la resolución de problemas.

Los puntos, en orden, que sigue una secuencia PARA la RP son:

1- Esto se hace así. 2- Ejercicios sin contexto. 3- Ejercicios con contexto, pero les llamamos “problemas”. 4- Con suerte, en una secuencia PARA la RP se proponen problemas de aplicación interesantes.

Nada más sencillo que tomar un libro de texto para comprobar esa secuencia. En la mesa tengo un bestseller de 2º de la ESO donde se identifican los tres primeros puntos. El cuarto, ni está ni se le espera.

Los autores parecen ser conscientes de la pérdida de tiempo que supone todo esto. En el margen: no te preocupes, ahora haz, que ya si eso, el curso que viene, los dominarás.

Este gif es por el tweet de antes. No, no los dominarán. He visto alumnado de bachillerato con dificultades enormes para distinguir las medidas estadísticas obtenidas de una tabla de frecuencias de los parámetros de una distribución.

Y alumnado que solo ha llegado a la varianza a partir de la tabla de frecuencias, con el xi^2fi^2. OMG. ¿Estamos locos? Que sí, que son menos cuentas, pero para llegar a esa fórmula coges un atajo de los gordos. Y en educación matemática, lo interesante suele estar en el camino.

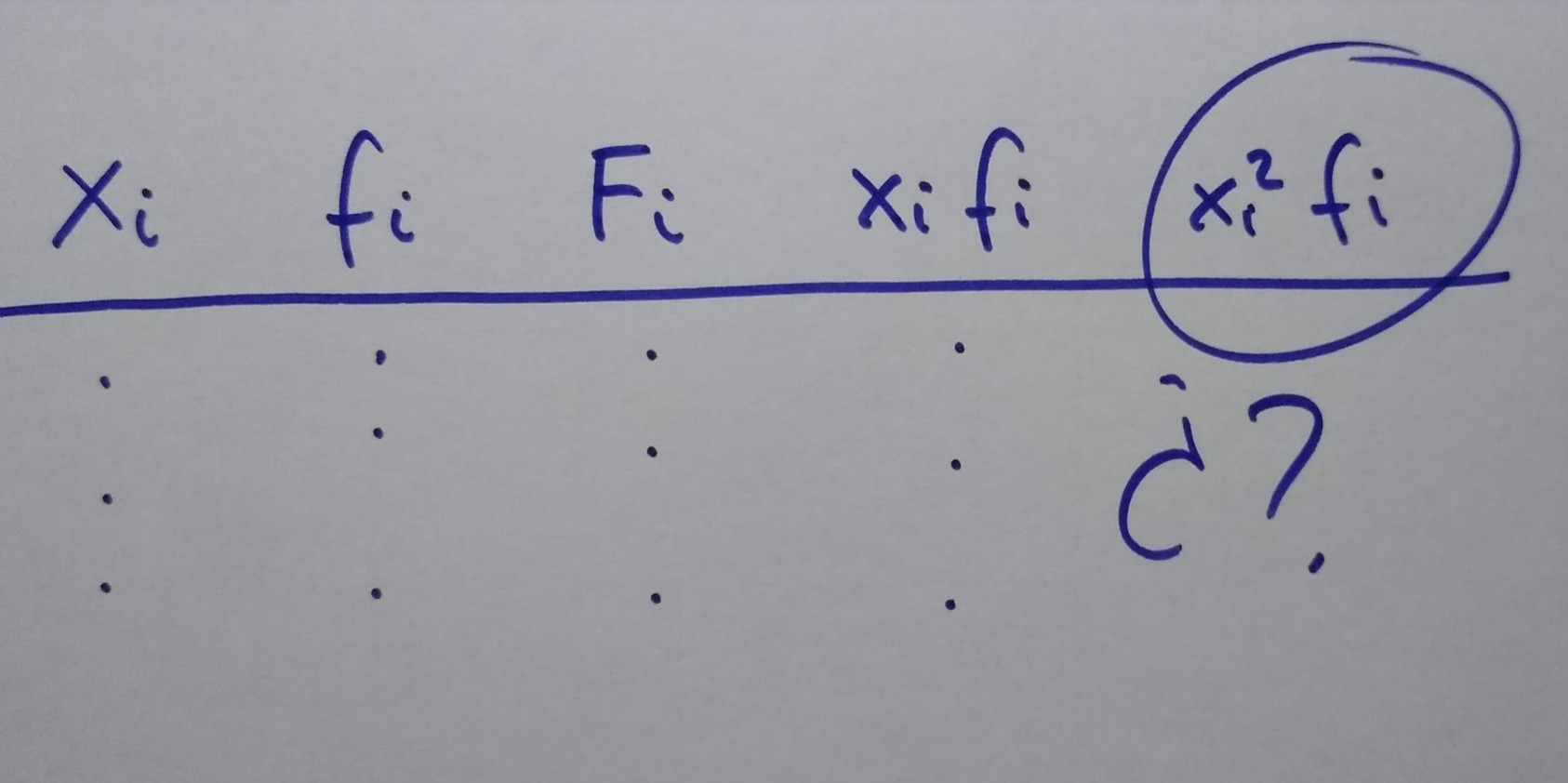
Para llegar a esa fórmula se realizan ciertas manipulaciones algebraicas, utilizando propiedades nada triviales de la varianza y la esperanza. Que a veces se nos olvida la O de la ESO. Que tenemos que intentar, como docentes, que cada alumno alcance su máximo potencial.

Añadiendo de entrada una carga simbólica innecesaria para mostrar la idea de dispersión, nos estamos dejando atrás a muchos alumnos. Y casi todos los que consiguen sobrellevar con “éxito” la secuencia, habrán aprendido unas reglas y poco más.

Bromas aparte, algo bueno es que el libro presenta la desviación media. Visto el currículo, peor habría sido ver el rango porque sí y a otra cosa, que es lo que especifica al concretar los estándares de aprendizaje evaluables. El cómo lo hace es otra historia.

Todo mi respeto por los autores de los libros de texto. Entiendo que lo normal será estar condicionado por una línea editorial, restricciones en número de páginas y otros factores que desconozco.

¿La comprensión de la dispersión mejora con la mera repetición de ejercicios? No. Desde la didáctica de la matemática hay herramientas que permiten analizar la idoneidad de secuencias de enseñanza y aprendizaje y reflexionar sistemáticamente sobre ellas.

Indicadores de una elevada idoneidad a nivel de contenidos, sin entrar mucho en detalle: muestra representativa de situaciones-problema, articulación de diferentes registros y representaciones lingüísticas (verbal, gráfico, simbólico, etc.), modelización, problematización, …

Precisamente, en el último número de AIEM (revista de la @_seiem) hay un artículo que analiza la enseñanza de las medidas de dispersión en libros de texto de educación secundaria (3º y 4º ESO). Los resultados señalan las carencias de los libros de texto.

Hemos hablado sobre libros de texto. Son un recurso más y su uso depende de la competencia profesional del docente. Faltaría más. Sin embargo, marcan mucho el camino a seguir. Demasiado. Tanto, que algunos autores hablan de ellos como el currículo de facto. Y eso no puede ser.

Si ponemos el piloto automático con el libro, por comodidad, o porque nos empujan a ello las políticas educativas (horas lectivas, ratios, falta de formación en didáctica específica), hemos de ser conscientes de la escasa idoneidad del proceso de enseñanza y aprendizaje.

La enseñanza a través de la RP es rica, exigente y apasionante. Todo parece indicar su gran potencial, pero sigue siendo una línea abierta de investigación. Los dibujines y los gifs corren a cuenta de mi hermanita @creacionesbjara. ¿A que son geniales? 🔚