Conexión decimal-fracción, con tortillas, unpacked
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.
- 4,99… es aproximadamente 5
- No, es que es 5.
- ¿Ein?
Conexión decimal-fracción. Con tortillas. Unpacked.

Sí, hay varias maneras de razonar. Por ejemplo, trata de buscar un número entre el 4,99… y el 5, complicado, ¿verdad? O toma 10 veces el 4,99… y quítale una vez el 4,99…, con lo que tienes 9 veces el 4,99… O con series geométricas.
Pero este hilo no va de eso. Y como buena pregunta cebo, se responderá al final. Voy a tratar de mostrar ejemplos de tareas que comenzarían en primaria y que culminarían en 3º ESO aprox.
Me gusta hablar de tareas porque se trata de hacer. Y mientras se hace, se piensa y se le da significado a lo que se hace. Y se discute. En definitiva, se construye conocimiento a partir de la resolución de situaciones y problemas. No se presenta a las mates como un monumento.
Si habéis leído los hilos de multiplicación y división de fracciones, recordaréis que hablaba de medida. Es decir, las fracciones representaban cantidades de magnitud u operadores que actuaban sobre esas cantidades.
Pues bien, ahora cambiamos las gafas para meternos en el modelo de reparto. El numerador va a indicar el número de objetos a repartir (hablaré de tortillas) y el denominador el número de participantes (hablaré de personas).
Como los objetos a repartir tendrán que ser fraccionables, este significado de la fracción como reparto no está aislado del de medida. Hay un control del tamaño de los trozos que se reparten.
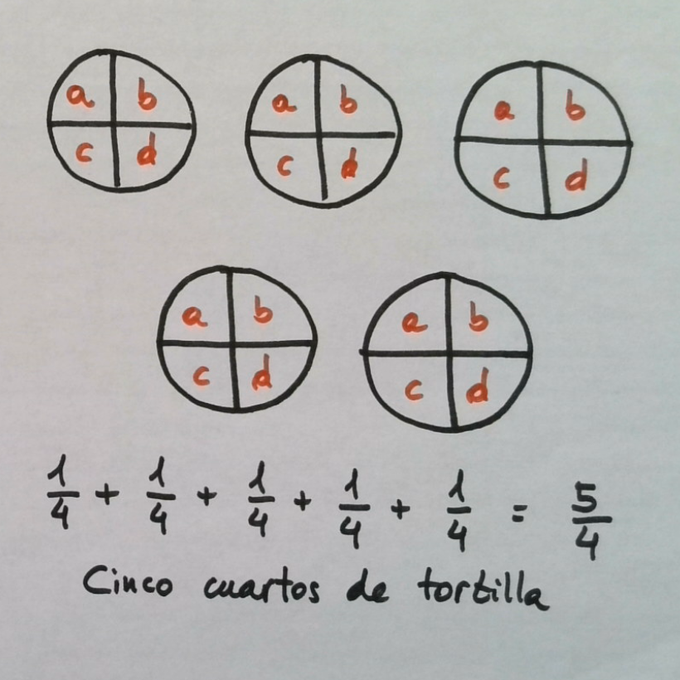
Con $5/4$ simbolizaremos, por tanto, dos cosas. Por un lado, el reparto en sí; es decir, el proceso de repartir 5 tortillas para 4 personas. Por otro lado, la cantidad de tortilla que recibirá cada uno de los participantes.

Reparte de forma equitativa 5 tortillas entre 4 personas, al menos, de 3 formas distintas. Intenta explicarlo de manera verbal, gráfica y simbólica. No te hagas spoiler y piénsalo.

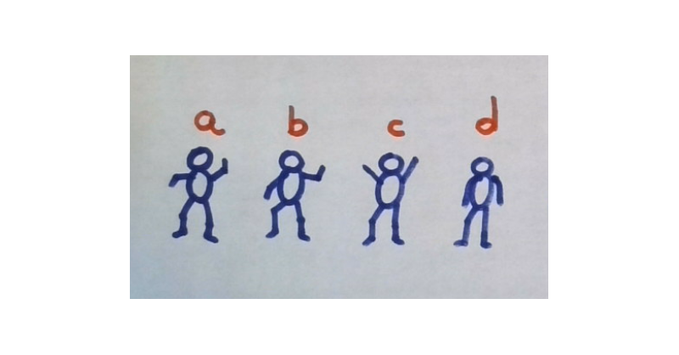
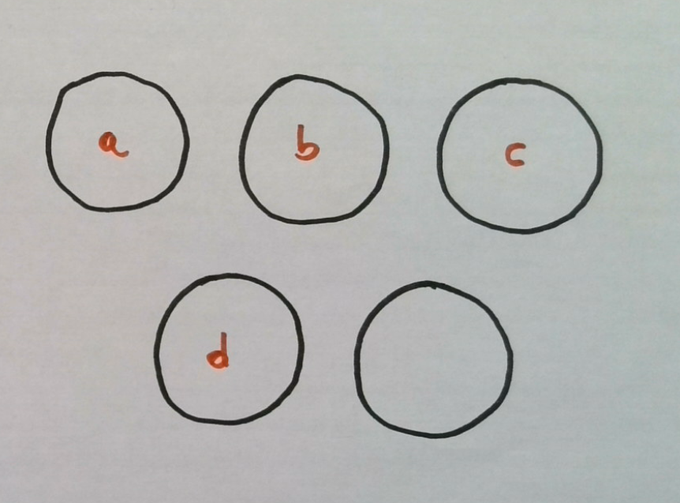
Puede que digas… ¡Qué fácil! Parto cada tortilla en cuatro trozos iguales y a cada participante le doy un trozo de esos de cada tortilla. Venga, os presento a los participantes (soy original y los llamo a, b, c y d ) y en el siguiente tuit lo muestro gráfica y simbólicamente.
Eso es, aquí está. Cada uno recibe 5/4 de tortilla. ¿Pensamos otra manera?
Si en lugar de partir cada tortilla en cuatro, las parto en ocho trozos, a cada uno le tocarán dos trozos (octavos) de cada tortilla.
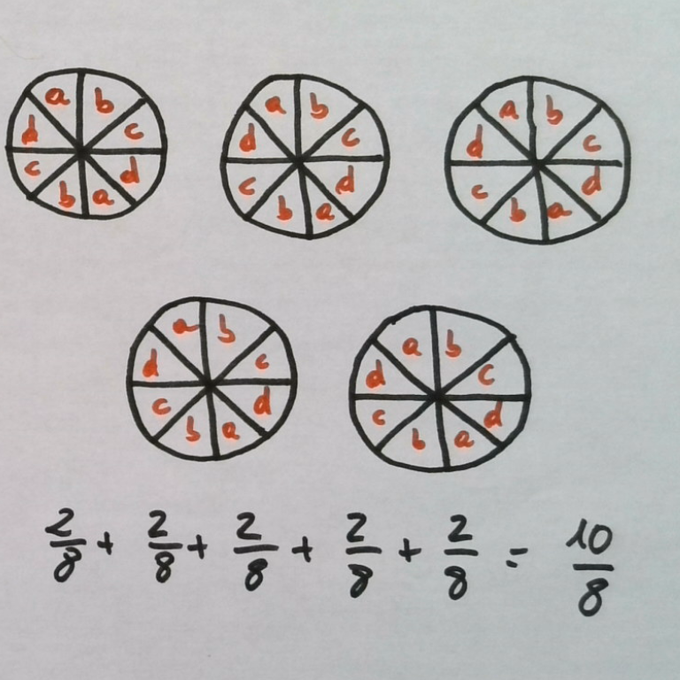
Sí, reciben la misma cantidad. En el primero $5/4$ y en el segundo $10/8$. ¿Puede decirse que son «iguales» esas fracciones? Representan la misma cantidad de tortilla, pero el proceso ha sido distinto.
Pero vaya tontada, Pablo. Y si las parto en 16 ya tengo otra forma, que pedías tres. Veamos, tanto el de cuartos como el de octavos los hemos hecho en una sola fase. ¿Qué ocurre si quiero dar tortillas enteras en este caso? Porque aquí podríamos, ¿no?
En una primera fase, daría una tortilla a cada participante.
Y después, en una segunda fase, esa tortilla que sobra, la partiría en 4 (si quiero terminar ya), y daría uno de esos trozos a cada participante. Cada uno recibiría una tortilla entera y un cuarto. Es decir, $1+1/4$.
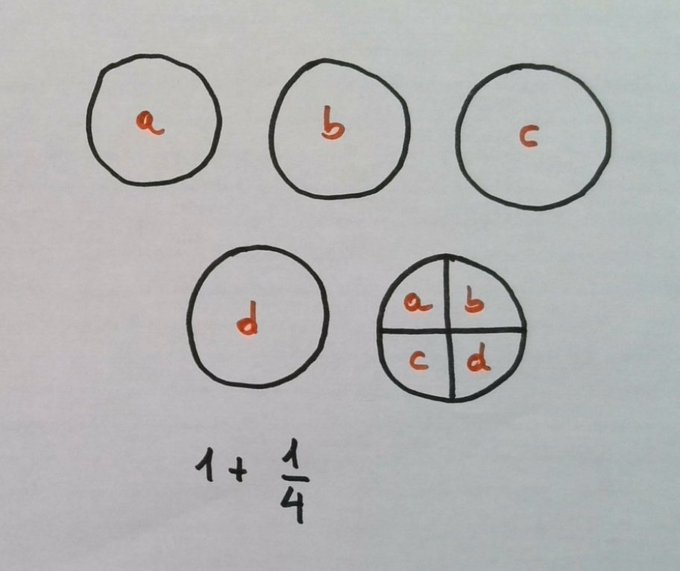
Como ejercicio, os propongo que la última tortilla no la dividáis en cuartos, sino en quintos. Os saldrá, por lo menos, una fase más.
La exploración de estos repartos ya da pie a interesantes discusiones de aula y movilización de contenidos, como la equivalencia de expresiones aritméticas.
Veamos ahora qué pasa si en cada fase no partimos lo que sobra de cualquier manera, sino que imponemos la condición de partirlo en 10 trozos (siempre iguales, eh, aunque en los dibujines se vea todo muy cutre).
Recuerdo. Cinco tortillas para cuatro personas. Primera fase, reparto tortillas enteras. Una a cada persona, doy en total cuatro y me sobra una. Usaré corchetes para indicar el tamaño de los trozos que estoy repartiendo.

Vamos con la segunda fase. Parto lo que sobra en 10 trozos iguales, por lo que ahora tendré 10 décimas (10 trozos de tamaño 1/10). Puedo dar 2 décimas a cada uno, dando en total 8 décimas. Me sobrarán 2 décimas por repartir.
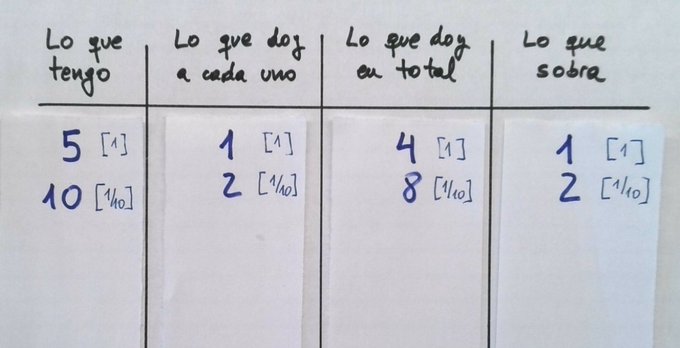
Sigue sobrando, por lo que hacemos una tercera fase. Parto esas dos décimas en 10 trocitos cada una, por lo que paso a tener 20 trocitos de tamaño 1/100. A cada uno le doy 5 de esos trocitos, dando en total 20 y no me sobra nada.

Por lo tanto, cada participante recibe 1 tortilla entera, dos trozos de tamaño $1/10$ de tortilla y cinco trozos de tamaño $1/100$. Según la tabla que hemos hecho, podemos escribirlo así:
$1+2[1/10]+5[1/100]$
Cuando algunos hablamos del papel de los algoritmos tradicionales, que hay que repensarlo y todo eso, es por esto. No sé cuántos os estáis dando cuenta de que esto es UNA DIVISIÓN DE LAS DE TODA LA VIDA. Cuando lo cuento en ESO o en magisterio, resulta que no es tan evidente.
Los algoritmos tradicionales pueden ser estupendos para profundizar en el sistema decimal posicional. Trabajarlos de forma machacona no lleva a ningún sitio, pero desde el significado, con manipulables, etc. llegamos a sitios maravillosos. CONTINÚO.
Hemos dado $1,25$ de tortilla a cada uno. Efectivamente, UNA tortilla entera, DOS décimas y CINCO centésimas. Aquí tenéis la primera fila de la tabla, la primera fase del reparto, con significado, según la división en caja.
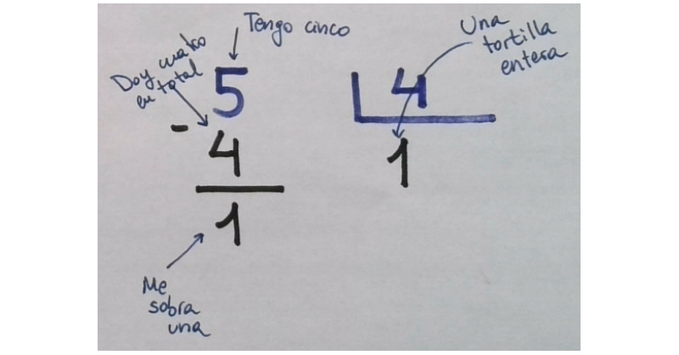
¿Alguien se ha preguntado alguna vez que es eso de bajar un cero? ¿De dónde se bajan? ¿De las nubes? Pues hala, aquí veis que es el comienzo de la segunda fase del reparto, me ha sobrado una tortilla entera y la parto en diez, por lo que tendré que repartir DÉCIMAS.
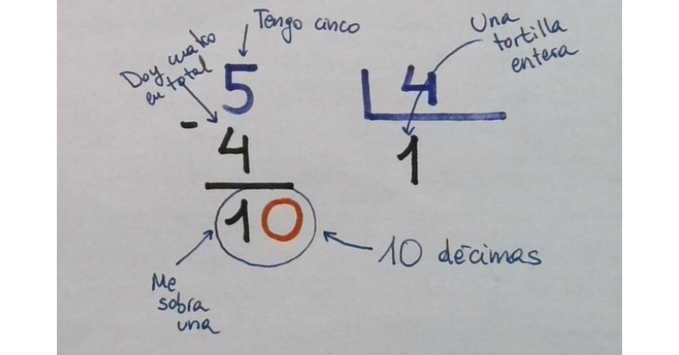
Y aquí está el final de la segunda fase. Tengo 10 décimas, puedo dar dos a cada participante, doy en total ocho, y me sobran dos DÉCIMAS por repartir.
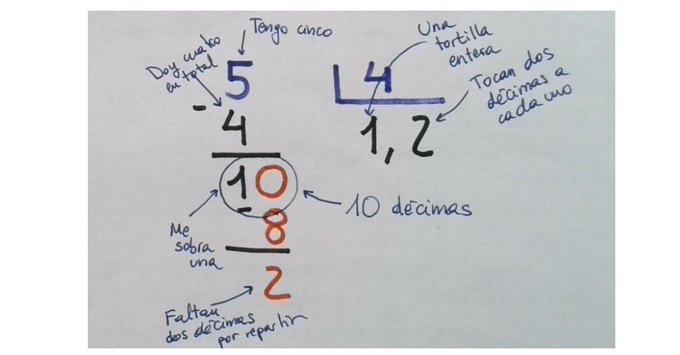
En la siguiente fase, parto las décimas en 10 trocitos cada una, por lo que tendré 20 centésimas a repartir entre 4 participantes. Tocan a 5 CENTÉSIMAS y no sobra ninguna.
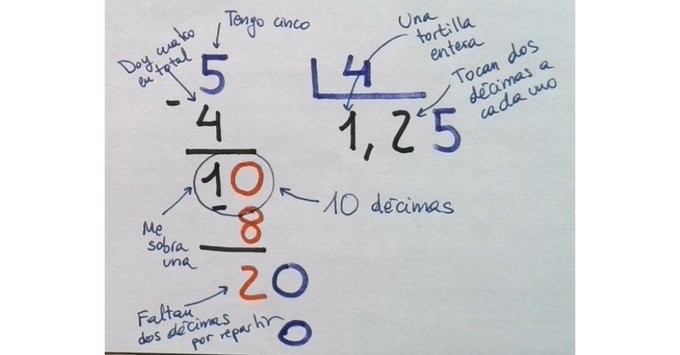
Ya hemos establecido la conexión fracción con decimal. Decía que todo esto culmina en 3º ESO. Hasta llegar a ese momento, podemos incorporar situaciones en las que se consideren diferentes repartos.
Si pensamos en el 5 tortillas para 3 personas, veremos que el reparto decimal no termina nunca. Pero, ¿eso quiere decir que cada uno recibe una cantidad infinita de tortilla? No, porque ya hemos visto que cada uno recibe siempre una cantidad equivalente a $5/3$ de tortilla.
Algo que se puede investigar, muy interesante, es ver cuáles son las condiciones para que se dé lo que ocurre con el cinco para tres, es decir, que el proceso sea infinito (vamos, que salgo periódico).
Y venga, ahora empezamos a enlazar con la pregunta cebo. Un problema interesante es preguntarse por las condiciones iniciales de un reparto; es decir, el número de tortillas y el número de participantes, sabiendo la cantidad de tortilla que ha recibido cada uno.
Primer caso. La representación polinómica decimal es finita (o sea, número con decimales fijos). Por ejemplo, supongamos que cada participante recibe 2 tortillas enteras y 3 décimas, es decir, $2,3$ tortillas. Llamaré «a» al número de tortillas y «b» al de participantes.

En la primera fase, por tanto, tengo a tortillas. Como me dicen que cada uno recibe dos tortillas, y hay $b$ participantes, en total habré dado $2b$ tortillas. Me sobra lo que tenía al principio menos lo que he dado. $a-2b$ tortillas.

Corto lo que me sobra en 10 trocitos, por lo que tendré $10(a-2b)$ trocitos, es decir $10a-20b$ trocitos de tamaño $1/10$ (décimas). Doy tres a cada uno, dando en total $3b$ décimas (multiplico por el nº de participantes, $b$, que es desconocido).
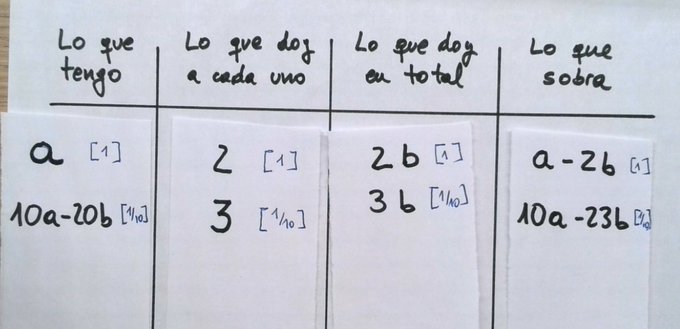
Pero espera, porque el reparto terminaba ahí. No sobraba nada… por lo que $10a-23b$ tiene que ser cero. Por lo tanto, las condiciones iniciales eran 23 tortillas y 10 personas. O cualquier reparto equivalente, como el 230 para 100.
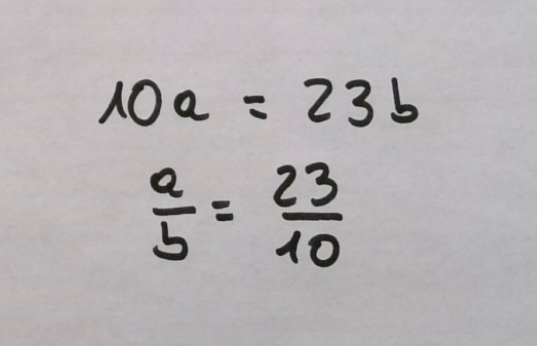
Segundo caso. Cuando la representación polinómica decimal es infinita (números periódicos). Si has hecho divisiones o ejemplos como los que ponía antes, sabrás que te sale periódico y tienes que parar cuando se empiezan a repetir los restos, las partes sobrantes.
Intentemos averiguar las condiciones iniciales de un reparto en el que cada participante recibe 1 tortilla entera, 3 décimas, 3 centésimas, 3 milésimas, etc. Es decir, 1,33.. tortillas.
Podría seguir ad infinitum, pero el caso es que sé que las partes sobrantes se están repitiendo. De hecho, en este caso, son todas iguales. Voy a igualar las dos primeras.
$10a-13b = a-b$

Por lo tanto, las condiciones iniciales eran 12 tortillas y 9 personas, o cualquier reparto equivalente, como $4/3$. Observemos que si hubiésemos igualado $a-b$ con $100a-133b$ también nos habría salido. Y también si igualamos $10a-13b$ con $100a-133b$.
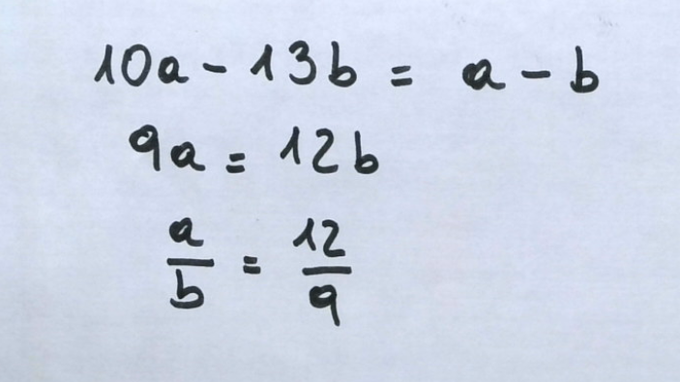
Si te has perdido en este punto, vuelve a donde se relaciona lo de la tabla (el reparto) con la división en caja. Ponte a dividir 12 entre 9 y trata de identificar el momento en que te das cuenta que “entras en bucle” y por qué.
Aquí irían diferentes situaciones. Cuando el período tiene más de una cifra resulta que los restos no son todos iguales, sino que van salteados. Cuando es periódico mixto, por ejemplo, se empiezan a repetir a partir de cierto momento…
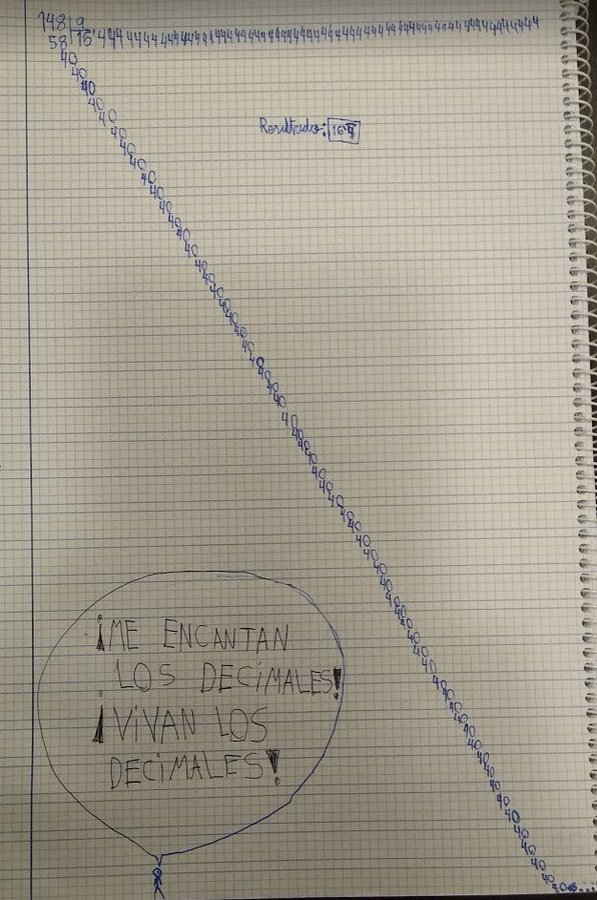
Y el momento genial, ¡aha!, cumbre o como queráis llamarlo viene cuando pides encontrar las condiciones iniciales del reparto en que cada uno recibe $4,99…$ tortillas. Para mí, uno de los mejores momentos de toda la ESO.
Voy a merendar, que con tanta tortilla me ha entrado el gusanillo. Así, si alguien quiere hacerlo, tiene un ratito.
Venga, ¿empezamos?

Como lo que sobra es siempre igual, $a-4b$ tiene que ser igual a $10a - 49b$. Si hiciese una fila más, lo que sobrase también sería igual.
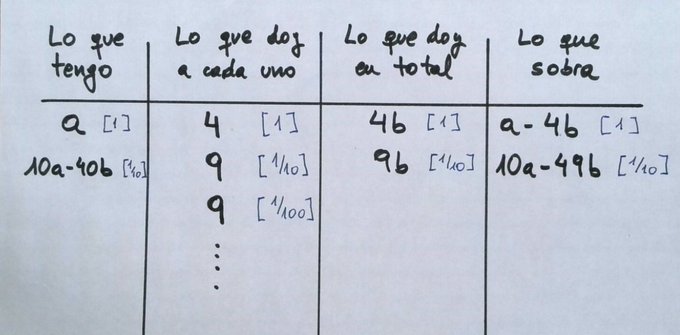
Y hete aquí que sale $45/9$; es decir, 45 tortillas para 9 personas, o 5 tortillas para una persona. En este momento:
- Pablo, ya lo he hecho pero creo que lo tengo mal. No puede ser. Me sale cinco.
ESE ES EL MOMENTO.
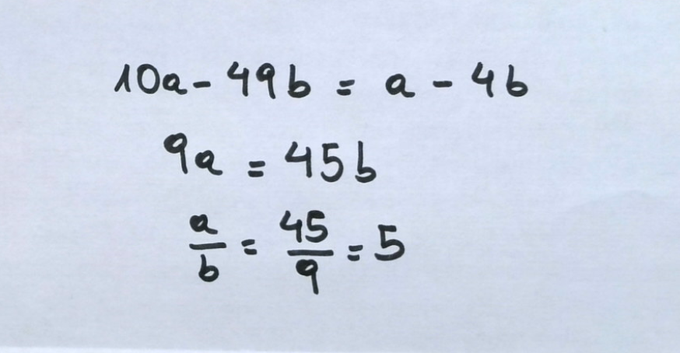
¿Qué está pasando? ¿Cómo va esto de las representaciones decimales que acaban en 9 período? Aquí es donde tienen lugar unas cuantas discusiones y charlas de aula. La idea de fondo es que las representaciones polinómicas decimales que vienen de un reparto son únicas. Salvo…
… salvo en las representaciones finitas, ya que también admiten otra representación a base de nueves periódicos. Y esta noción, la de que un mismo número admite diferentes representaciones, es fundamental.
Como decía al principio, formas de argumentar sobre representación decimal y fraccionaria hay muchas. Si queremos que el alumnado vea la fracción como número no podemos dejar que el peso de la secuencia en el parte-todo. Este modelo dificulta esa conexión. Enlace para saber más
Y sobre todo. Esto no se explica. Se hace, y mientras se hace, se reflexiona sobre lo que se está haciendo.
Esta cuestión está desarrollada en el fantástico libro «Números y algoritmos» de Gairín y Sancho. Y las trabajamos dentro de la asignatura Didáctica de la aritmética II en @FacultadEducaUZ @dm_unizar #cosicasdeDAII.
Algunos me habéis preguntado por la notación de corchetes. Es herencia de Gairín y compañía y es la que usamos en @FacultadEducaUZ @dm_unizar. Se trata de enfatizar el control de los trozos. Da pie a un trabajo simbólico mayor que no he puesto en este hilo.
De hecho, para dejar más claro que es un significado diferente del de medida, en Didáctica de la aritmética II lo que se hace es escribir $(a,b)$ en lugar de $a/b$ cuando estamos con los repartos.
Para curiosos: $(2,3)[1/10]$, en cierta fase de un reparto, indicaría que tengo 2 trozos, de tamaño $1/10$, a repartir entre 3 personas.
Dejo aquí unos hilos de hace poco: